Wolfram|Alpha ist ein großartiges Werkzeug zur Berechnung von Stammfunktionen und bestimmten Integralen, Doppel- und Dreifachintegralen und uneigentlichen Integralen. Es bietet außerdem Plots, alternative Darstellungen und andere relevante Informationen, die Ihre mathematische Intuition steigern.
Online Integralrechner
Integrale lösen mit Wolfram|Alpha
Mehr als nur ein Online-Integrallöser
Erfahren Sie mehr
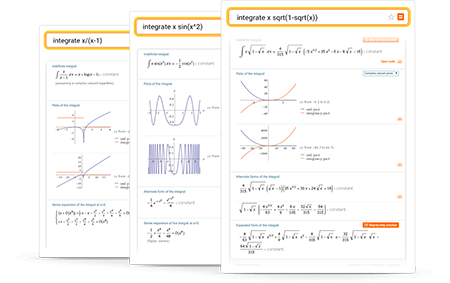
Tipps zur Eingabe von Abfragen
Geben Sie Ihre Abfragen in englischer Sprache ein. Um mehrdeutige Abfragen zu vermeiden, setzen Sie, wo nötig, Klammern. Hier sind einige Beispiele, die illustrieren, wie Sie ein Integral abfragen.
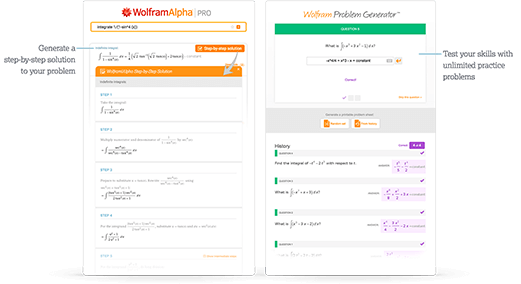
Access instant learning tools
Get immediate feedback and guidance with step-by-step solutions for integrals and Wolfram Problem Generator
Erfahren Sie mehr
Was sind Integrale??
Die Integralrechnung ist ein wesentlicher Bestandteil der Analysis zur Bestimmung der Stammfunktion oder des Flächeninhalts unter einer Kurve.
Das unbestimmte Integral von f(x), notiert als int f(x) dx, ist definiert als die Stammfunktion von f(x). Anders ausgedrückt, die Ableitung von int f(x) dx ist f(x). Da die Ableitung einer Konstante Null ist, sind unbestimmte Integrale nur bis zu einer beliebigen Konstante definiert. Beispielsweise ist int sin(x) dx = -cos(x) + Konstante, da die Ableitung von -cos(x) + constant sin(x) ist. Das bestimmte Integral von f(x) im Intervall x = a bis x = b, notiert als int_(a)^(b)f(x) dx, ist definiert als der positive und/oder negative Flächeninhalt zwischen f(x) und der x-Achse, von x = a bis x = b.
Stammfunktionen und Integrale sind durch den Fundamentalsatz der Analysis verbunden. Dieser besagt: Ist f(x) integrierbar über [a,b] und F(x) deren stetige Stammfunktion, dann gilt int_(a)^(b) f(x) dx = F(b) - F(a). Daraus folgt int_(0)^(pi) sin(x) dx = (-cos(pi))-(-cos(0)) = 2. Manchmal ist es nötig, das bestimmte Integral näherungsweise zu berechnen. Zu diesem Zweck werden häufig dünne Rechtecke unter der Kurve platziert und die positiven und negativen Flächen addiert. Wolfram|Alpha kann eine Fülle von Integralen lösen.
Wie Wolfram|Alpha Integrale berechnet
Wolfram|Alpha berechnet Integrale auf andere Art als Menschen. Es ruft Mathematicas Integrate-Funktion auf, die auf umfassender mathematischer und berechnungsbezogener Forschungsarbeit basiert. Integrate bewältigt Integrale anders als Menschen. Es verwendet nämlich leistungsfähige, allgemeine Algorithmen, die häufig auf äußerst anspruchsvoller Mathematik aufbauen. Für gewöhnlich werden dazu eine Reihe unterschiedlicher Verfahren angewendet. Eines davon besteht darin, die allgemeine Form für ein Integral auszuarbeiten, diese Form zu differenzieren und Gleichungen nach unbestimmten symbolischen Parametern zu lösen. Sogar für relativ einfache Integranden können die so generierten Gleichungen hochkomplex sein und benötigen Mathematicas starke algebraische Rechenfähigkeiten. Ein anderes Verfahren, das Mathematica bei der Berechnung von Integralen anwendet, ist die Umwandlung der Integrale in verallgemeinerte hypergeometrische Funktionen mit anschließender Anwendung von Formelsammlungen zu diesen sehr allgemeinen mathematischen Funktionen.
Obwohl Wolfram|Alpha dank dieser mächtigen Algorithmen Integrale in sehr kurzer Zeit berechnen und eine Vielzahl spezieller Funktionen bewältigen kann, ist es dennoch wichtig, zu verstehen, wie ein Mensch Integralrechnungen durchführen würde. Aus diesem Grund bietet Wolfram|Alpha auch Algorithmen, um Integrationen Schritt für Schritt vorzunehmen. Diese Algorithmen wenden völlig andere Integrationstechniken an, die das manuelle Lösen eines Integrals nachahmen, einschließlich Integration durch Substitution, partieller Integration, trigonometrischer Substitution und Integration durch Partialbruchzerlegung.