Wolfram|Alpha ist ein nützlicher Rechner für erste, zweite und dritte Ableitungen, für Ableitungen an einer bestimmten Stelle sowie für partielle Ableitungen. Erfahren Sie mehr über Ableitungen und wie Wolfram|Alpha diese berechnet.
Online Ableitungsrechner
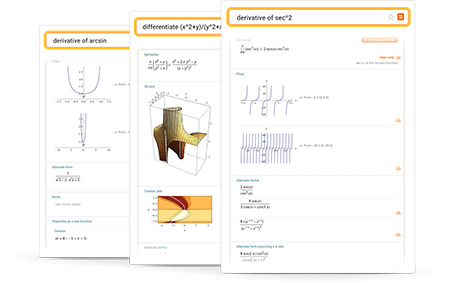
Ableitungen lösen mit Wolfram|Alpha
Mehr als nur ein Online-Ableitungsrechner
Erfahren Sie mehr
Tipps zur Eingabe von Abfragen
Geben Sie Ihre Abfragen in englischer Sprache ein. Um mehrdeutige Abfragen zu vermeiden, setzen Sie, wo nötig, Klammern. Hier sind einige Beispiele, die illustrieren, wie Sie eine Ableitung abfragen.
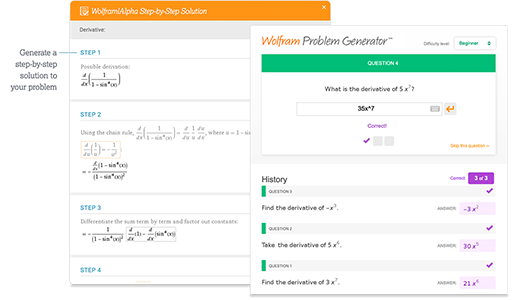
Access instant learning tools
Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator
Erfahren Sie mehr
Was sind Ableitungen?
Die Ableitung ist ein wesentlicher Bestandteil der Analysis und stellt eine infinitesimale Änderung einer Funktion und der damit verbundenen Variablen dar.
Ist eine Funktion f x gegeben, gibt es mehrere Notationsmöglichkeiten für die Ableitung von f nach x. Die geläufigsten Varianten sind d fd x und f'x. Bei n Ableitungen wird die Notation dn fdxn oder fnx verwendet. In diesem Fall spricht man von Ableitungen höherer Ordnung. Beachten Sie, dass Ableitungen zweiter Ordnung häufig als f''x notiert werden.
An der Stelle x = a ist die Ableitung definiert als f'a = limh0f a + h - f hh . Dieser Grenzwert existiert nicht in allen Fällen, aber wenn er existiert, dann sagt man, dass f x differenzierbar an der Stelle x = a ist. Geometrisch entspricht f'a der Tangentensteigung von f x an der Stelle x = a.
Ist zum Beispiel f x = x3, dann ist die erste Ableitung f'x = limh0h+x3-x3h = 3x2 und wir können f''x berechnen:f''x = limh03x+h2-3 x2h = 6x. Die Ableitung ist ein wichtiges Werkzeug mit zahlreichen Anwendungen. Mit ihrer Hilfe lassen sich zum Beispiel lokale/globale Extremwerte und Wendepunkte bestimmen, Optimierungsprobleme lösen und die Bewegung von Objekten beschreiben.
Wie Wolfram|Alpha Ableitungen berechnet
Wolfram|Alpha ruft Mathematicas D Funktion auf, die auf eine größere Zahl an Identitäten zurückgreift, als in einem handelsüblichen Analysis-Lehrbuch enthalten sind. Dabei wird auf „altbekannte“; Regeln wie die Linearität der Ableitung, die Produktregel, Potenzregel, Kettenregel etc. zurückgegriffen. Zusätzlich verwendet D auch „weniger bekannte“ Regeln zur Berechnung der Ableitung einer Vielzahl spezieller Funktionen. Bei Ableitungen höherer Ordnung sind Regeln wie die allgemeine Produktregel imstande, den Berechnungsprozess zu beschleunigen.